가상 면접 사례로 배우는 대규모 시스템 설계 기초 (System Design Interview) - 저 : 알렉스 쉬, 역 : 이병준 을 읽고 정리한 글입니다.
6 장에서는 비 관계형 데이터베이스라 불리우는, 키-값 저장소에 대해서 이야기하면서 아래 조건에 해당되는 키-값 저장소를 분산 시스템에서의 조건으로 설계해봅니다.
1. 키-값 쌍의 크기는 10KB 이하이다.
2. 큰 데이터를 저장할 수 있어야 한다.
3. 높은 가용성을 제공해야 한다. 따라서 시스템은 설사 장애가 있더라도 빨리 응답해야한다.
4. 높은 규모 확장성을 제공해야한다. 따라서 트래픽 양에 따라 자동적을 ㅗ서버 증설/삭제가 이루어져야 한다.
5. 데이터 일관성 수준은 조정이 가능해야 한다.
6. 응답 지연시간(latency)은 짧아야한다.
➡️ 6장은 내용이 길고 좋은 내용이 많아서 2개로 나누고자 합니다.
- 1파트는 : 분산 시스템을 설계하는데 알아야할 CAP 이론에 대해서
- 2파트는 : 키-값 저장소 설계에 사용되는 핵심 컴포넌트들에 대해서
1파트에서 키-값 저장소 설계의 기본 개념과 분산 서비스를 설계하는데 알아야할 CAP정리에 대한 내용을 정리했습니다.
이번 포스팅에서는 6장의 남은 내용인 "키-값 저장소 구현에 사용될 핵심 컴포넌트들 및 기술들"에 대해서 정리합니다.
[목차]
- 데이터 파티션
- 데이터 다중화(replication)
- 일관성 (consistency)
- 일관성 불일치 해소 (inconsistency resolution)
- 장애 처리
- 시스템 아키텍처 다이어그램
- 쓰기 경로 (write path)
- 읽기 경로 (read path)
📌 01. 데이터 파티션
대규모 어플리케이션에서 전체 데이터를 한 대 서버에 욱여넣는 것은 불가능하다고 합니다.
이러한 문제를 해결하는 가장 단순한 해결책이 "데이터 파티셔닝" 입니다.
데이터 파티션이란
- 데이터를 "작은 파티션"들로 분할한 다음 여러 대 서버에 저장하는 것 입니다.
데이터를 파티션 단위로 나눌 떄는 다음 2가지 문제를 중요하게 생각해야합니다.
- 데이터를 여러 서버에 고르게 분산할 수 있는가
- 노드가 추가되거나 삭제될 떄 데이터의 이동을 최소화 할 수 있는가
→ 5장에서 이야기한 "안정해시" 는 이러한 파티션 문제를 해결하는 적합한 기술입니다.
안정해시를 사용하여 데이터 파티션 시 장점
- 규모화장 자동화 (auto scaling) - 시스템 부하에 따라 서버가 자동으로 추가되거나 삭제되도록 만들 수 있습니다. (해시 링의 특성)
- 다양성 : 각 서버의 용량에 맞게가상 노드의 수를 조정할 수 있습니다. (고성능 서버는 더 많은 가상노드를 갖도록)
📌 02. 데이터 다중화
높은 가용성과 안정성을 확조하기 위해서 데이터를 N개 서버에 비동기적으로 다중화할 필요 있습니다.
N개의 서버를 선정하는 방법
- 어떤 키를 해시 링 위에 배치한 후, 그 지점으로 링을 순회하면서 만나는 첫 N개 서버에 데이터 사본을 보관합니다.
- 그런데 가상 노드를 사용하면 선택한 N개의 노드가 대응될 실제 물리 서버의 개수가 N보다 작아지는 문제가 생길 수 있습니다.
이 문제를 피하려면 노드를 선택할 때 같은 물리 서버를 중복 선택하지 않도록 해야 합니다.
- 같은 데이터 센터에 속한 노드는 정전, 네트워크 이슈, 자연재해 등의 문제를 동시에 겪을 가능성 있습니다.
- 따라서 안정성을 담보하기 위해 데이터의 사본은 다른 센터의 서버에 보관하고, 센터들은 고속 네트워크로 연결
📌 03. 데이터 일관성
여러 노드에 다중화된 데이터는 적절히 동기화 되어야 합니다.
다중화된 노드에 데이터를 분산 저장할 때, 정족수 합의 (Quorum Consensus) 알고리즘을 이용해서 일관성 수준을 조절할 수 있습니다.
💡 정족수 합의 정의
- N = 사본 개수
- W = 쓰기 연산에 대한 정족수. 쓰기 연산이 성공한 것으로 간주되려면 적어도 W개의 서버로부터 쓰기 연산이 성공했다는 응답을 받아야 한다.
- R = 읽기 연산에 대한 정족수. 읽기 연산이 성공한 것으로 간주되려면 적어도 R개의 서버로부터 응답 받아야 한다.
다음은 N=3일 때 key1을 통해서 val1을 서버에 저장할 때 예시 입니다.
참고로 중재자는 클라이언트와 노드 사이의 Proxy이며, 노드가 중재자가 되는 경우도 있습니다.
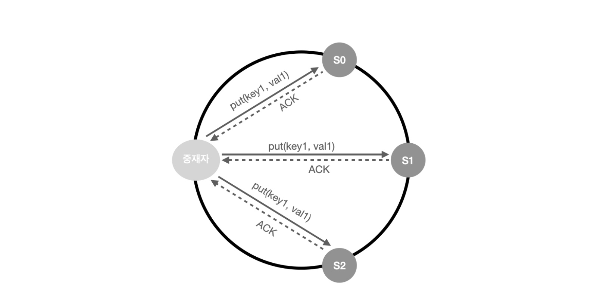
- W=1인 경우,
- 데이터가 한 대 서버에만 기록된다는 뜻이 아닙니다.
- 쓰기 연산이 성공했다고 판단하기 위해 중재자는 최소 한 대 서버로부터 쓰기 성공 응답을 받아야 한다는 뜻 입니다.
- W, R, N의 값을 정하는 것은 응답 지연과 데이터 일관성 사이의 타협점을 찾는 전형적인 과정입니다.
- W=1 또는 R-1인 구성의 경우 중재자는 한 대의 서버로부터의 응답만 받으면되니 응답 속도 빠름
- 1보다 큰 경우는 데이터의 일관성 수준이 향상되지만 응답 속도가 느려짐
- W + R > N인 경우 강한 일관성이 보장됨
그래서 이러한 조합을 이용하면 다음과 같은 경우들로 나눌수 있습니다.
- R = 1, W = N : 빠른 읽기 연산에 적합한 시스템
- R = N, W = 1 : 빠른 쓰기 연산에 적합한 시스템
- R + W > N : 강한 일관성이 보장
- R + W <= N : 강한 일관성이 보장되지 않음
💡 일관성 모델
강한 일관성(strong consistency)
- 모든 읽기 연산은 가장 최근에 갱신된 결과를 반환
- 클라이언트는 정대로 낡은 데이터를 보지 못함
- 가장 일반적인 방법은 모든 사본에 쓰기 연산 결과가 반영될 때까지 해당 데이터에 대한 읽기/쓰기를 금지
- 새로운 요청의 처리가 중단되기 때문에 고가용성 시스템에 부적합
약한 일관성(weak consistency)
- 읽기 연산은 가장 최근에 갱신된 결과를 반환하지 못할 수 있습니다.
최종 일관성(eventual consistency)
- 약한 일관성의 한 형태로, 갱신 결과가 결국에는 모든 사본에 반영(동기화) 되는 모델
- 쓰기 연산이 병렬적으로 발생하면 시스템에 저장된 값의 일관성이 깨질 수 있는데, 이 문제는 클라이언트가 해결해야 합니다.
- 클라이언트 측에서 데이터 버전 정보를 활용해 일관성이 깨진 데이터를 읽지 않도록 할수도 있습니다.
📌 04. 일관성 불일치 해소 방법
💡비 일관성 해소 기법 : 데이터 버저닝
데이터를 다중화하면, 가용성은 높아지지만 사본 간 일관성이 깨질 가능성이 높아집니다.
"버저닝"과 "벡터시계" 는 이러한 문제를 해소하기 위해 등장 기술입니다.
버저닝 (Versioning)
- 데이터를 변경할 때마다 해당 데이터의 새로운 버전을 만듦니다.
- 따라서, 각 버전의 데이터는 불변 (immutable)
벡터 시계(vector clock)
- [서버, 버전]의 순서쌍을 데이터에 메단 것
- 어떤 버전이 선행, 후행인지, 충돌이 있는지 판별하는데 사용됩니다.
- D([S1, v1], [S2, v2], ..., [Sn, Vn])와 같이 표현한다고 가정합니다.
- D는 데이터
- 데이터 D를 서버 Si에 기록하면 아래 작업 가운데 하나를 수행해야 합니다.
- [Si, Vi]가 있으면 Vi를 증가시킴
- 그렇지 않으면 새항목 [Si, 1]를 만듦
- 어떤 버전 X와 Y 사이에 충돌이 있는지 보려면 Y의 벡터 시계 구성요소 가운데 X의 벡터 시계 동일 서버 구성요소보다 작은 값을 갖는 것이 있는지 보면 됩니다.
- D([s0, 1], [s1, 2])와 D([s0, 2], [s1, 1])는 서로 충돌
👏🏻 구체적인 사례
- 클라이언트가 데이터 D1을 시스템에 기록.
- 이 연산을 처리한 서버는 Sx. 벡터 시계는 D1([Sx, 1])으로 변함
- 다른 클라이언트가 D1을 읽고 D2로 업데이트한 다음 기록.
- D2는 D1을 덮어씀. 쓰기 연산은 같은 서버 Sx가 처리한다면 벡터 시계는 D2([Sx, 2])로 변함
- 다른 클라이언트가 D2를 읽어 D3로 갱신한 다음 기록.
- 이 연산은 Sy가 처리한다면 벡터 시계 상태는 D3([Sx, 2], [Sy, 1])로 바뀜
- 또 다른 클라이언트가 D2를 읽어 D4로 갱신한 다음 기록.
- 이 연산은 Sz가 처리한다면 벡터 시계 상태는 D4([Sx, 2], [Sz, 1])
- 어떤 클라이언트가 D3와 D4를 읽으면 데이터 간 충돌이 있다는 것을 알게됨. D2를 Sy와 Sz가 각기 다른 값으로 바뀌었기 때문,
- 따라서 클라이언트가 충돌 해소 후 서버에 기록.
- 이 연산을 처리한 서버는 Sx일 경우 벡터 시계는 D5([Sx, 3], [Sy, 1], [Sz, 1])로 바뀜
단점
- 충돌 감지 및 해소 로직이 클라이언트에 들어가야 하므로, 클라이언트 구현이 복잡해집니다.
- [서버, 버전]의 순서쌍 개수가 굉장히 빨리 늘어납니다.
- 이 문제를 해결하려면 길이에 임계치를 설정하고, 임계치 이상으로 길이가 길어지면 오래된 순서쌍을 벡터 시계에서 제거
- 하지만 이렇게 하면 버전 간 선후 관계가 정확하게 결정될 수 없기에 충돌 해소 과정의 효율성이 낮아짐
- 하지만 다이나모 디비에 관련된 문헌에 따르면, 아마존은 실제로 문제가 벌어진 적은 없음
📌 05. 장애 감지
서버의 장애는 아주 흔하게 발생하므로, 장애를 감지하고 해소하는게 중요하다.
분산 시스템에서의 장애 감지
- 보통 서버 A가 죽어도 바로 A 장애를 처리하지 않고, 두 대 이상의 서버가 똑같이 서버 A의 장애를 보고해야 해당 서버에 실제로 장애가 발생했다고 간주합니다.
- 모든 노드 사이에 멀티캐스팅 채널을 구축하는 것이 서버 장애 감지하는 가장 손쉬운 방법 입니다.
- 하지만 서버가 많을 때는 비효율적입니다.
- 가십 프로토콜같은 분산형 장애감지 솔루션을 채택하는 것이 더 효율적입니다.
💡가십 프로토콜(gossip protocol)
- 분산형 장애 감지 솔루션
동작 원리
- 각 노드는 멤버십 목록을 유지. 멤버십 목록은 각 멤버 ID와 그 박동 카운터(heartbeat counter) 쌍의 목록
- 각 노드는 주기적으로 자신의 박동 카운터를 증가시킴
- 각 노드는 무작위로 선정된 노드들에게 주기적으로 자기 박동 카운터 목록을 보냄
- 박동 카운터 목록을 받은 노드는 멤버십 목록을 최신 값으로 갱신
- 어떤 멤버의 박동 카운터 값이 지정된 시간 동안 갱신되지 않으면 해당 멤버는 장애 상태(Offline)인 것으로 간주
📌 06. 장애 처리
1) 일시적 장애 처리
- 가십 프로토콜로 장애를 감지한 시스템은 가용성을 보장하기 위해 필요한 조치를 해야 함
- 엄격한 정족수 접근법을 사용하면 읽기와 쓰기 연산을 금지해야 합니다.
- 느슨한 정족수 접근법은 이 조건을 완화하여 가용성을 높입니다.
- 정족수 요구사항을 강제하는 대신, 쓰기 연산을 수행할 W개의 건강한 서버와 읽기 연산을 수행할 R개의 건강한 서버를 해시 링에서 고름
- 장애 서버로 가는 요청은 다른 서버가 잠시 맡아 처리
- 그동안 발생한 변경사항은 해당 서버가 복구되었을 때 일괄 반영해 일관성 보존
- 이를 위해 임시로 쓰기 연산을 처리한 서버에는 그에 관한 단서를 남깁니다.
- 이런 장애 처리 방안을 단서 후 임시 위탁(hinted handoff) 기법이라 부릅니다.
→ 정족수란, 부산시스템에서 작업을 수행하기 위해 분산 트랜잭션이 얻어야하는 최소 투표수 입니다.
2) 영구 장애 처리
- 반-엔드로피(anti-entropy) 프로토콜을 구현하여 사본들을 동기화 합니다.
- 사본들을 비교해 최신 버전으로 갱신하는 과정을 포함 합니다.
- 사본 간의 일관성이 망가진 상태를 탐지하고 전송 데이터의 양을 줄이기 위해 머클(Merkle) 트리 사용합니다.
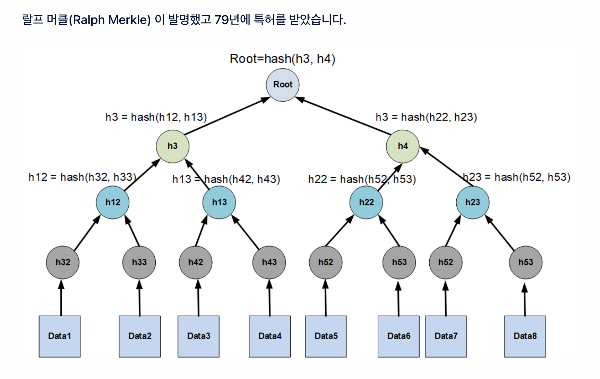
머클(Merkle) 트리
- 암호학이나 컴퓨터 과학에서 머클 트리(Merkle tree) 란 모든 자식 노드들이 암호학적 해시로 이뤄진 데이터 블록을 갖는 트리 형태의 자료 구조로 해시 트리(hash tree)라고도 부릅니다.
- 각 노드에 그 자식 노드들에 보관된 값의 해시(자식 노드가 종단 노드인 경우), 또는 자식 노드들의 레이블로부터 계산된 해시 값을 레이블로 붙여두는 트리
- 대규모 자료 구조의 내용을 효과적이면서도 보안상 안전한 방법으로 검증할 수 있습니다.
👏🏻 Git 이 머클트리를 사용해서 버전관리를 합니다.
동작 원리
- 키 공간을 버킷으로 나눔
- 버킷에 포함된 각각의 키에 균등 분포 해시 함수를 적용해 해시 값 계산
- 버킷 별로 해시값을 계산한 후, 해당 해시 값을 레이블로 갖는 노드 생성
- 자식 노드의 레이블로부터 새로운 해시 값을 계산해, 이진 트리를 상향식으로 구성해나감
- 각 머클 트리의 비교는 루트 노드의 해시 값을 비교하는 것으로 시작
- 루트 노드의 해시 값이 일치하면 두 서버는 같은 데이터를 가짐
- 다른 데이터를 갖는 버킷을 찾고 그 버킷들만 동기화
3) 데이터 센터 장애 처리
- 데이터를 여러 데이터 센터에 다중화하는 것이 중요
요약
| 목표/문제 | 기술 |
| 대규모 데이터 저장 | 안정 해시를 사용해 서버들에 부하 분산 |
| 읽기 연산에 대한 높은 가용성 보장 | 데이터를 여러 데이터센터에 다중화 |
| 쓰기 연산에 대한 높은 가용성 보장 | 버저닝 및 벡터 시계를 사용한 충돌 해소 |
| 데이터 파티션 | 안정 해시 |
| 점진적 규모 확장성 | 안정 해시 |
| 다양성(heterogeneity) | 안정 해시 |
| 조정 가능한 데이터 일관성 | 정족수 합의 |
| 일시적 장애 처리 | 느슨한 정족수 프로토콜과 단서 후 임시 위탁 |
| 영구적 장애 처리 | 머클 트리 |
| 데이터 센터 장애 대응 | 여러 데이터 센터에 걸친 데이터 다중화 |
📌 07. 시스템 아키텍처 다이어그램
지금까지는 키-값 저장소를 만드는데 고려해야할 다양한 기술적 문제들을 살표보았으니
이제 아키텍처 다이어그램을 그려봅니다.
아키텍처의 주된 기능은 다음과 같습니다.
- 클라이언트는 키-값 저장소가 제공하는 두 가지 get(key), put(key, value)와 통신한다.
- 중재자(coordinator)는 클라이언트에세 키-값 저장소에 대한 프락시 역할을 하는 노드다.
- 노드는 안정해시의 해시 링 위에 분포한다.
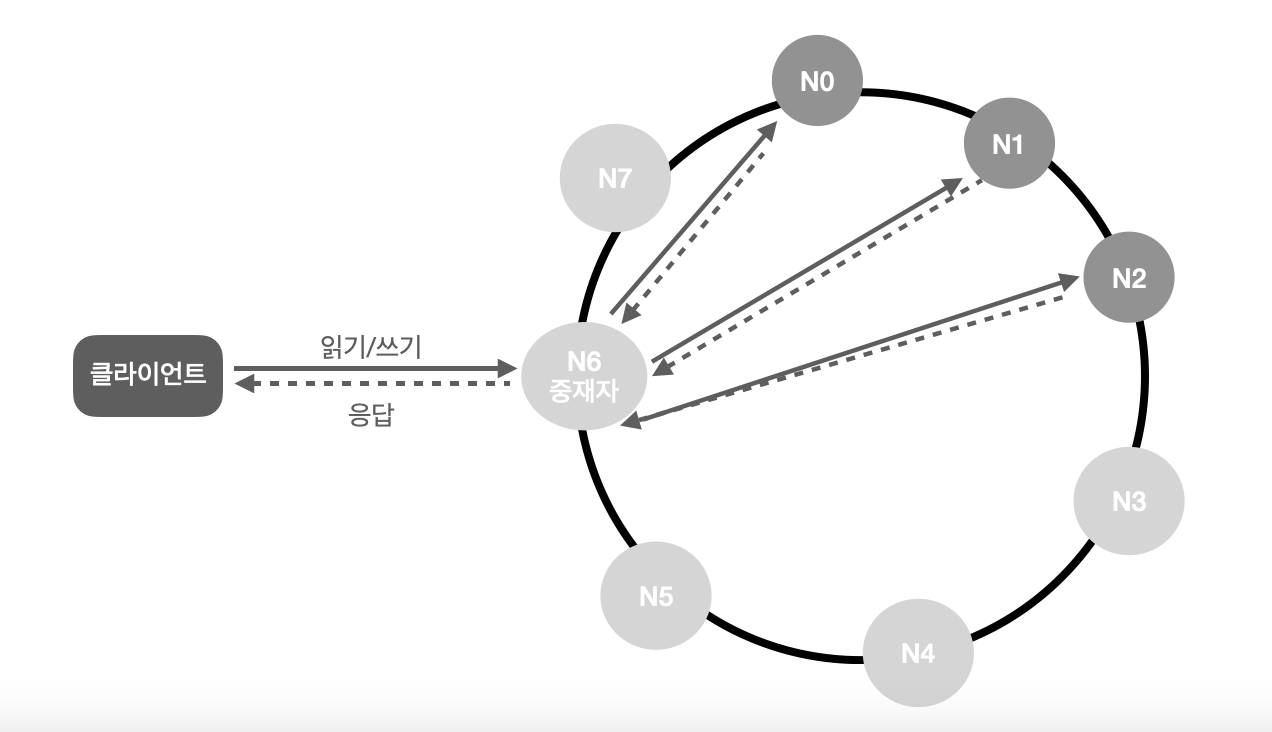
- 노드를 자동으로 추가, 삭제할 수 있도록 시스템은 완전히 분산된다.
- 데이터는 여러 노드에 다중화된다.
- 모든 노드가 같은 책임을 지므로 SPOF(Single Point of Failure)는 존재하지 않는다.
- 완전 분산 설계이므로, 모든 노드는 아래와 같은 기능 전부 지원해야 한다.
- 클라이언트 API
- 장애 감지
- 데이터 충돌 해소
- 장애 복구 매커니즘
- 다중화
- 저장소 엔진
쓰기 경로
- 쓰기 요청이 커밋 로그 파일에 기록됨
- 데이터가 메모리 캐시에 기록됨
- 메모리 캐시가 가득차거나, 임계치에 도달하면 데이터는 디스크에 있는 SSTable에 기록됨.
(Sorted-Srting Table의 약어, <키, 값>의 순서쌍을 정렬된 리스트 형태로 관리하는 테이블)
읽기 경로
- 데이터가 메모리 캐시에 있는지부터 살핌
- 메모리에 없는 경우는 디스크에서 가져옴
- 어느 SSTable에 찾는 키가 있는지 알아낼 효율적인 방법이 필요함
- 블룸 필터 사용됨
굉장히 많은 개념들이 진짜 깊이들어가지않고 개념들만 와르르 쏟아지니까 매우 힘들다;;
아무튼
끝!!

'📗 개발자 책 읽기 > 가상 면접 사례로 배우는 대규모 시스템 설계 기초' 카테고리의 다른 글
| [System Design Interview] 10. 알림 서버 시스템 설계하기 (0) | 2023.05.29 |
|---|---|
| [System Design Interview] 07. 분산 시스템 환경에서의 고유 유일 ID 값 생성하기 (feat UUID) (0) | 2023.05.29 |
| [System Design Interview] 06. ⚙️ 키-값 저장소 (비 관계형 데이터베이스) 설계하기(1) - CAP 이론 정리 (2) | 2023.01.16 |
| [System Design Interview] 05. ⚙️ 안정해시란? (0) | 2023.01.10 |
| [System Design Interview] 04. 트래픽 처리율 제한 장치의 설계 (rate limiter)❗️❗️ (2) | 2023.01.06 |